Major Activities
Last year, we have been working on the the theorectical part for pure machine learning (nDNN) and model-constrained deep learning approaches (mcDNN). The numerical results are provided for linear 1D inverse deconvolution problem, and 2D Heat equation. The mcDNN requires less training data to achieve the same accuracy level compared to nDNN. It is due to the fact that, for linear case, mcDNN has the data-driven form of Tikhonov inverse solver framwork, for non-linear problem, mcDNN is reinforced by the model-constrained term, and thus encodeing the physic. This year we develop the Tikonov neural network approach (TNet) and apply all approaches to more complicated problems (2D Burgers’ equations and 2D Navier-Stokes equation). We present and provide intuitions and rigorous results for TNet. The advantgeous features of Tnet are (1) requires a few observation samples and no need for true parameter of interest (PoI); (2) recovering exactly Tikhonov framework in the case of linear inverse problem (3) faster convergence rate (with fewer training samples) to Tikhonov’s accuracy level than mcDNN and nDNN.
More detail about this work can be found at https://arxiv.org/abs/2105.12033.
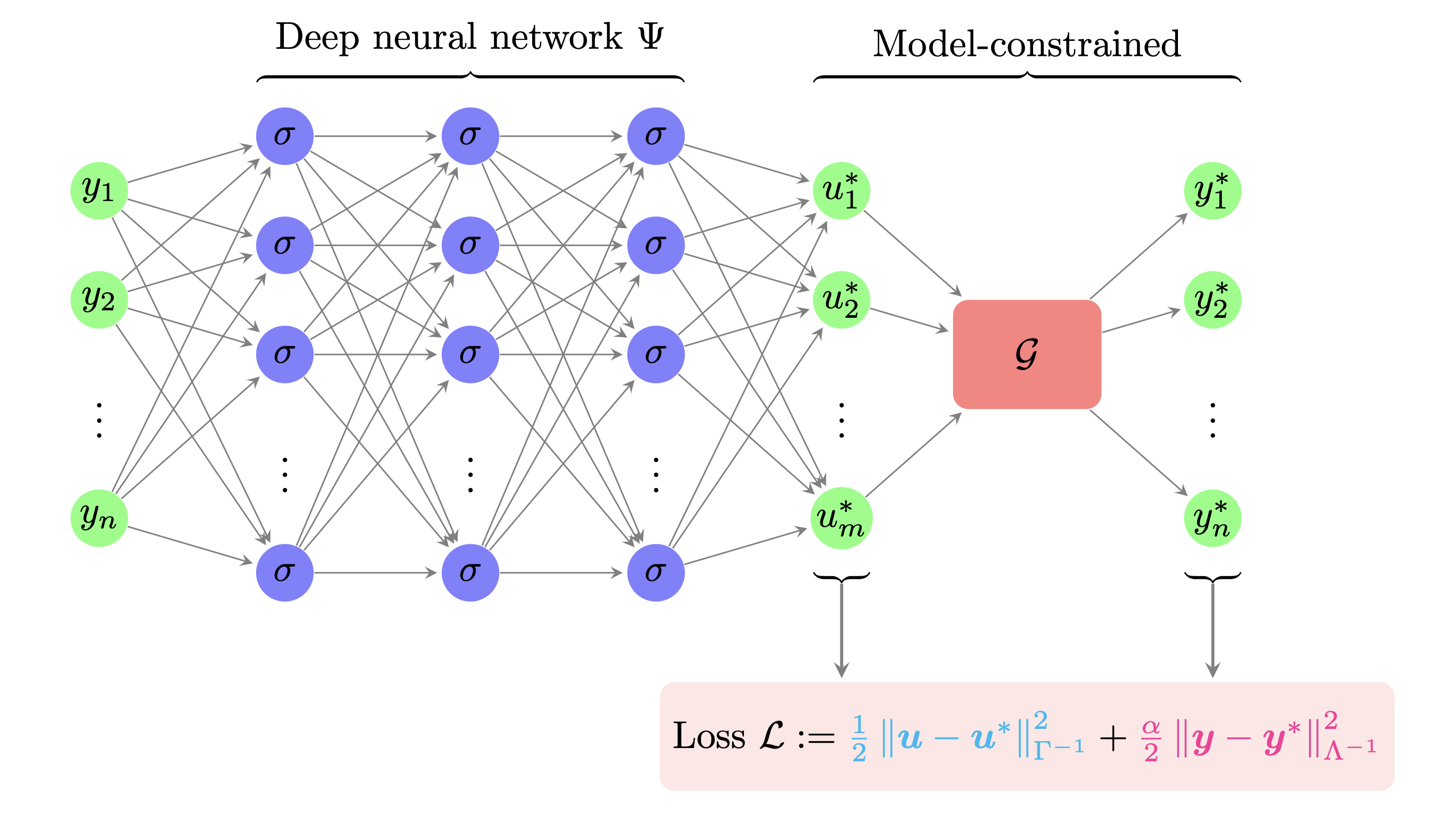Figure 1: Model-constrained neural network architecture mcDNN. The observables y is fed into the neural network Ψ. The parameter u∗ predicted by the netork is pushed through the PtO map G to generate the corresponding predicted observations y∗. Both predicted parameters and observations are compared with ground truth u and y, respectively, to provide the mean-square error in the loss function L..
Significant Results
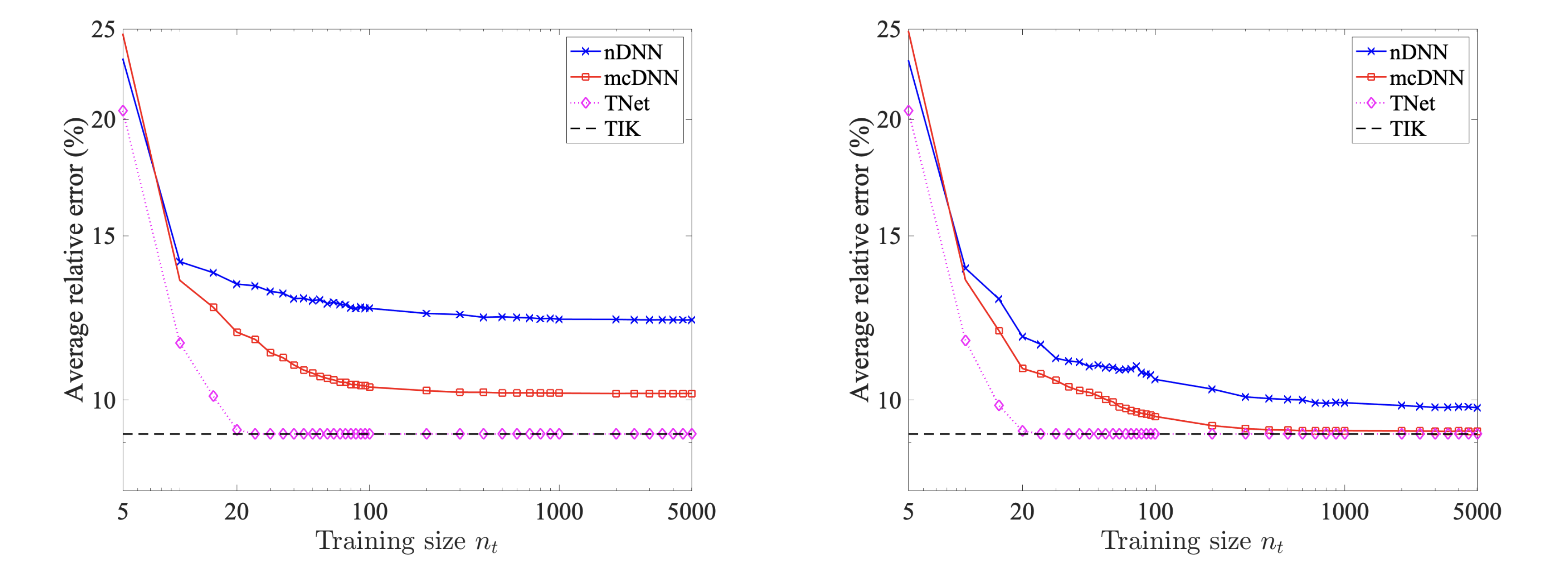Figure 2: 1D Linear deconvolution problem The average relative error at the optimal regularization parameter versus the training size for nDNN, mcDNN, TNet, and Tikhonov methods. The result for Case II (data augmentation technique) is on the left figure for training size up to $5000$, and a similar result is shown on the right figure for Case III (all distinct samples data).
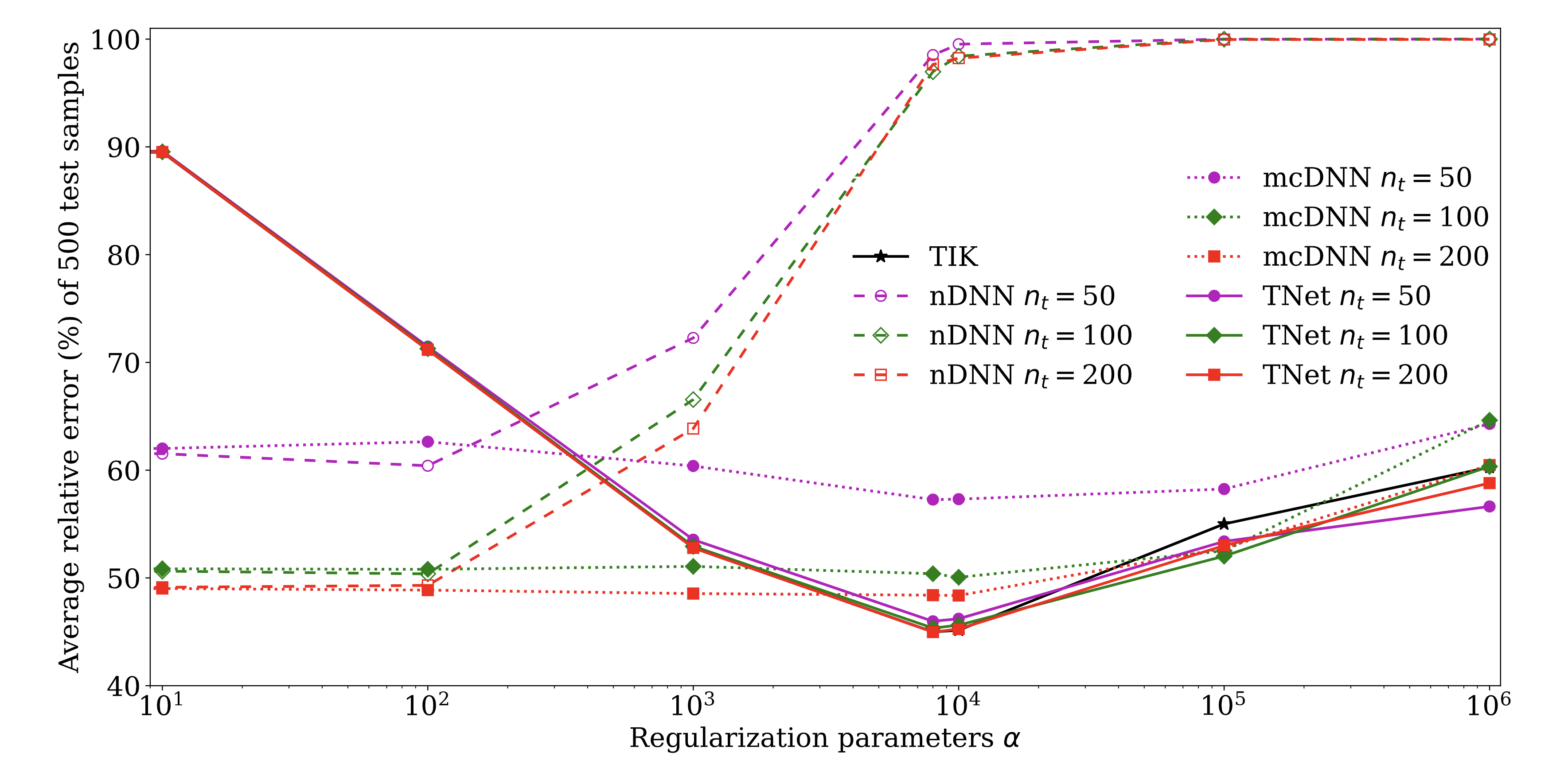Figure 3: 2D heat conductivity inverse problem The average relative error over 500 test samples. The comparisons are done for nDNN (dashed curves), mcDNN (dotted curves), TNet (colored solids curves), and Tikhonov (TIK: black curve) over a wide range of regularization parameter values.
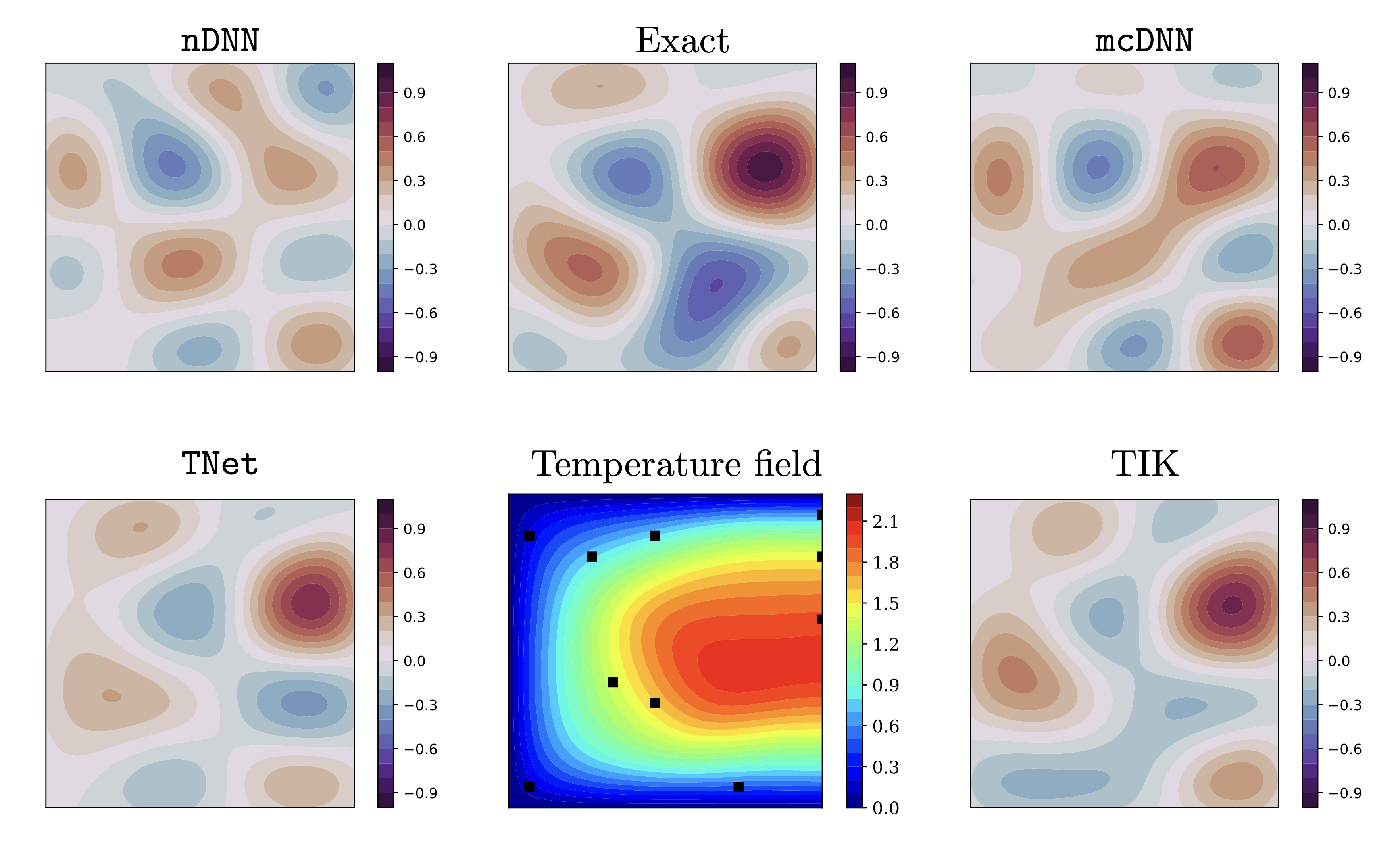Figure 4: 2D heat conductivity inverse problem Predicted (reconstructed) heat conductivities for an unseen noisy test sample obtained by nDNN, mcDNN, and TNet neural networks along with the Tikhonov reconstruction. Shown in the middle column are the synthetic ground truth (Exact) conductivity and the corresponding temperature field for reference.
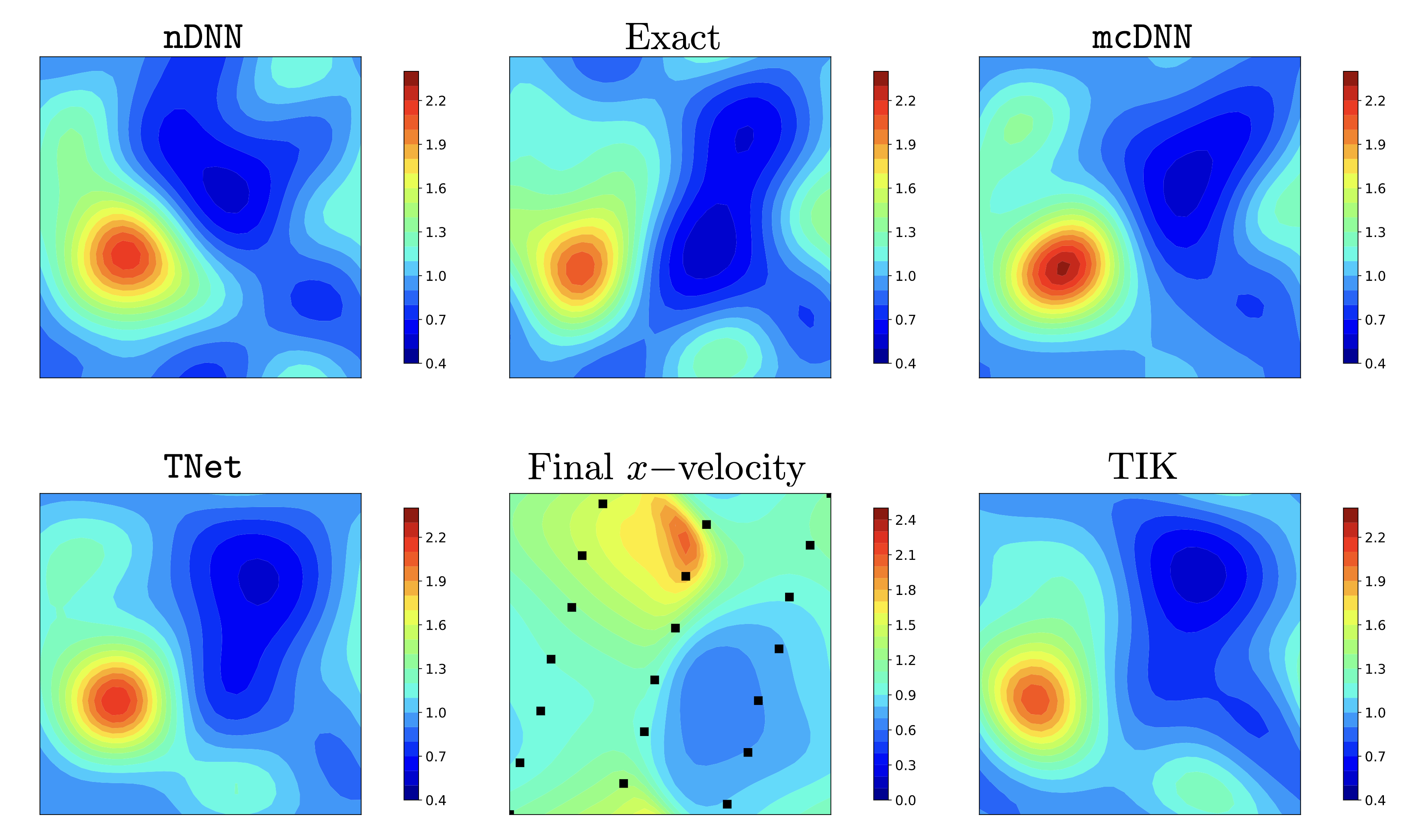Figure 5: 2D Burger's equations. Predicted (reconstructed) initial x-velocity component for an unseen noisy test sample obtained by nDNN, mcDNN, and TNet neural networks along with the Tikhonov reconstruction. Shown in the middle column are the synthetic ground truth (Exact) x-velocity and the corresponding x-velocity at the final time for reference.
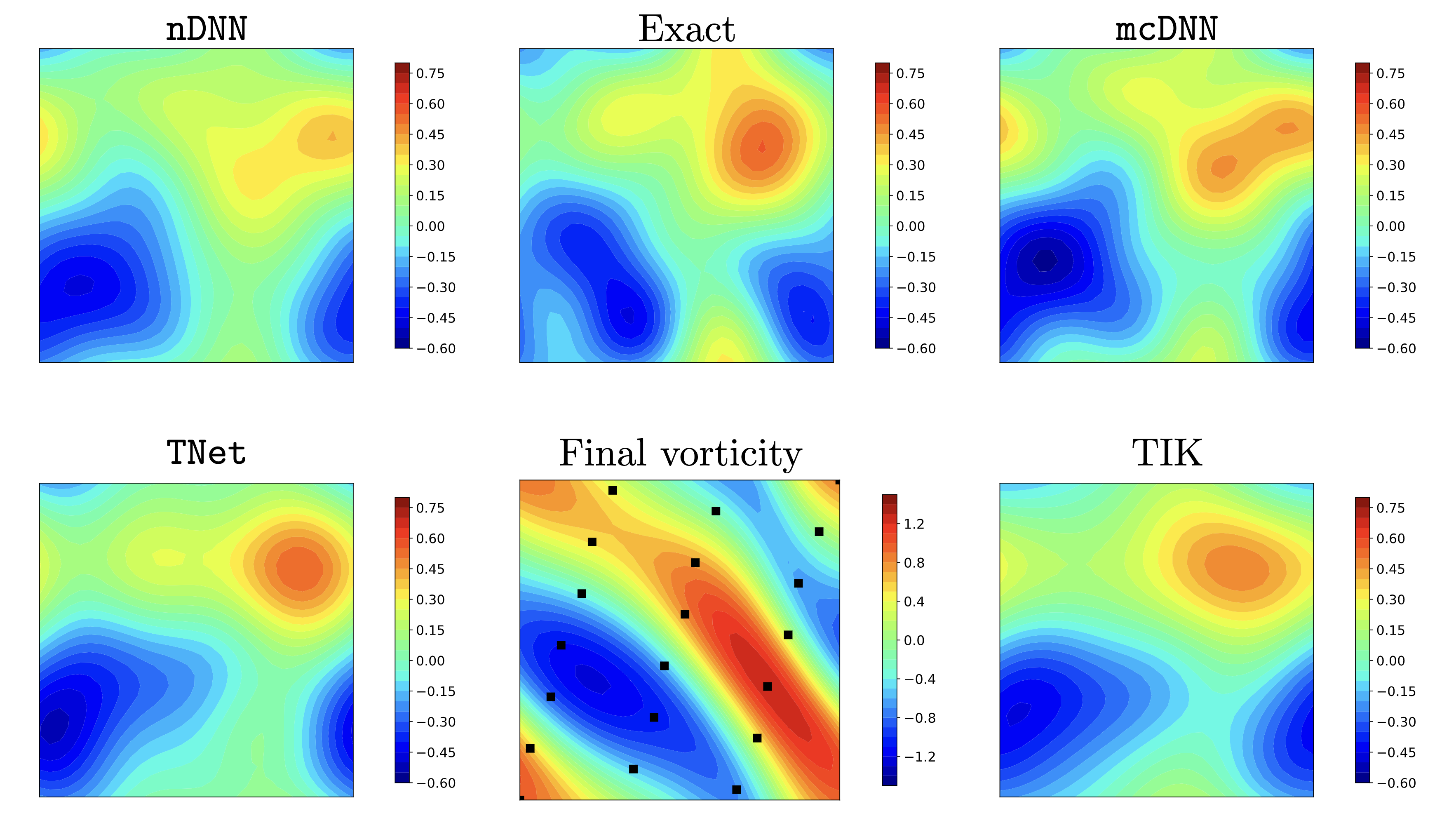Figure 6: 2D Navier-Stokes equation Predicted (reconstructed) initial vorticities for an unseen noisy test sample obtained by nDNN, mcDNN, and TNet neural networks along with the Tikhonov reconstruction. Shown in the middle column are the synthetic ground truth (Exact) vorticity and the corresponding vorticity at the final time for reference.