Major Activities
Last year, we have been working the theorectical part and most of promising numerical results are produced. This year we provided complete proof for the theorectical part and wrapped up the work for publication. This work has been published [paper]. The paper presents a regularization framework that aims to improve the fidelity of Tikhonov inverse solutions. At the heart of the framework is the data-informed regularization idea that only data-uninformed parameters need to be regularized, while the data-informed parameters, on which data and forward model are integrated, should remain untouched. We propose to employ the active subspace method to determine the data-informativeness of a parameter. The resulting framework is thus called a data-informed (DI) active subspace (DIAS) regularization. Four proposed DIAS variants are rigorously analyzed, shown to be robust with the regularization parameter and capable of avoiding polluting solution features informed by the data. They are thus well suited for problems with small or reasonably small noise corruptions in the data. Furthermore, the DIAS approaches can effectively reuse any Tikhonov regularization codes/libraries. Though they are readily applicable for nonlinear inverse problems, we focus on linear problems in this paper in order to gain insights into the framework. Various numerical results for linear inverse problems are presented to verify theoretical findings and to demonstrate advantages of the DIAS framework over the Tikhonov, truncated SVD, and the TSVD-based DI approaches
Significant Results
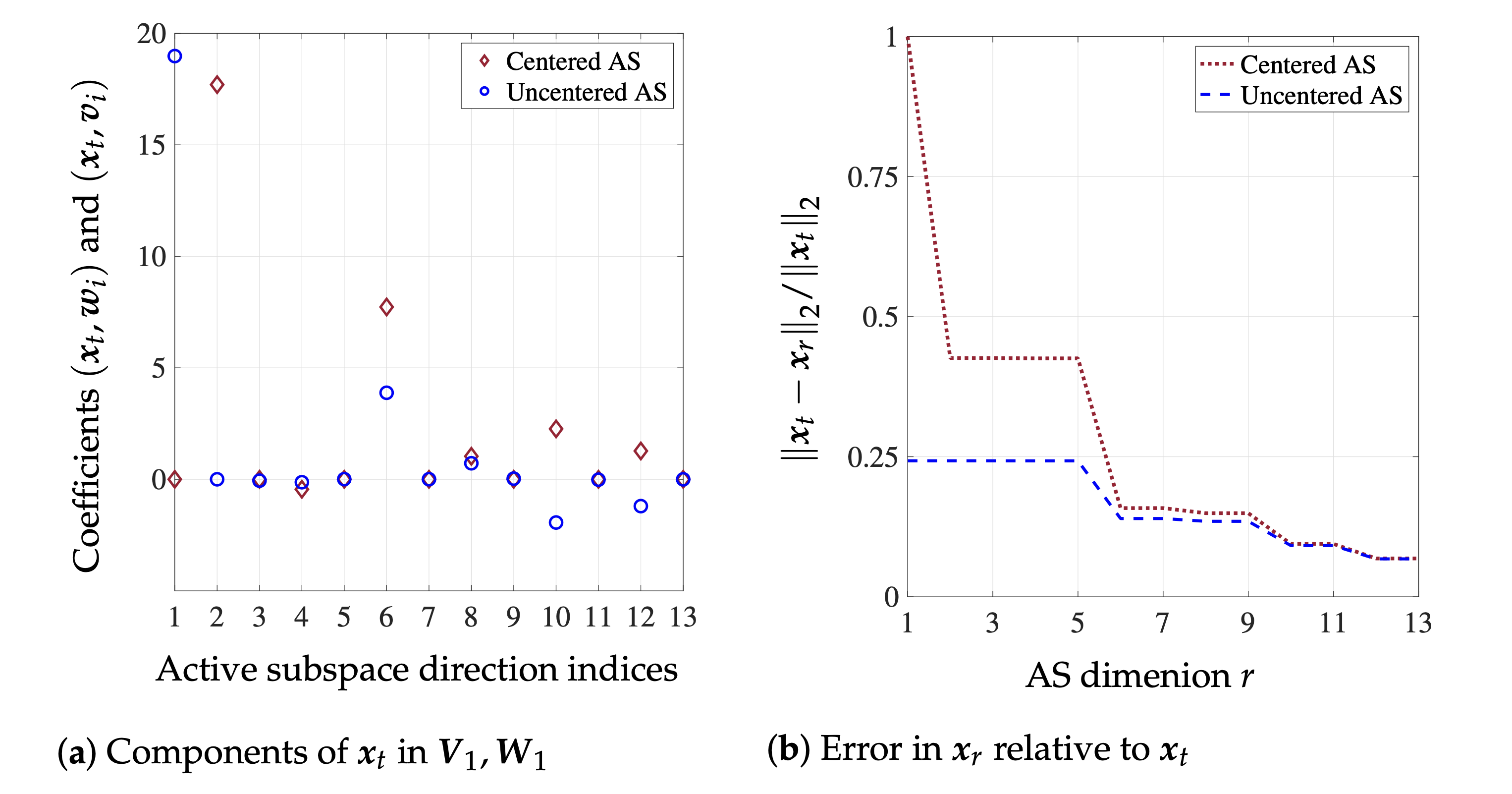Figure 1: 1D deconvolution problem. (Left): uncentered AS subspace versus centered AS subspace in representing the true solution. In the uncentered eigenspace, the true solution lies almost entirely in the first eigenmode, while it predominantly lies in the second and sixth modes of the centered eigenspace (Right): relative error of DIAS-A and TSVD solutions as a function of active subspace dimension r. Uncentered AS provides more accurate projection, even with one active direction (r = 1). Centered AS needs at least 10 active directions to start being comparable to the uncentered counterpart in terms of accuracy.
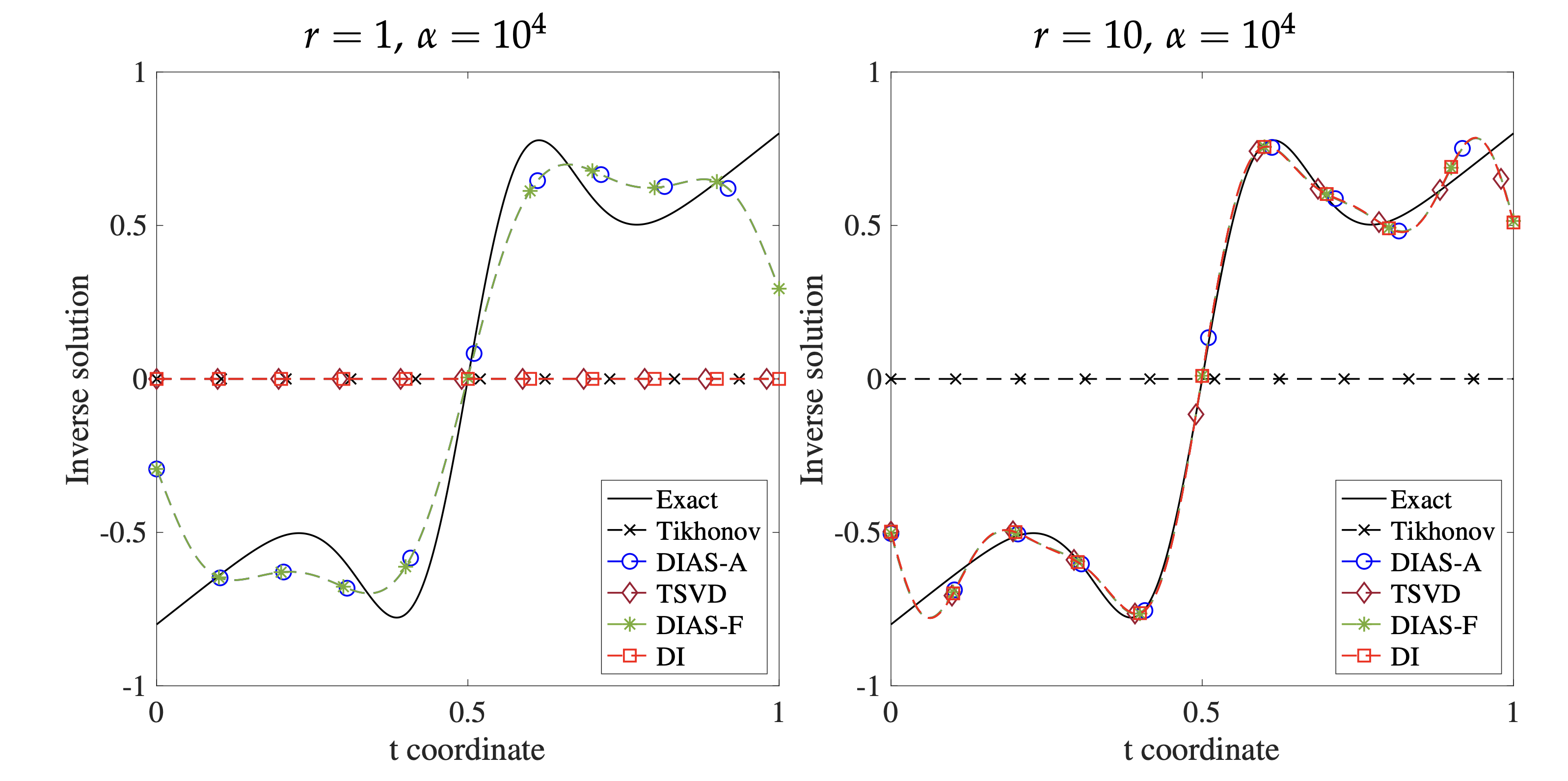Figure 2: 1D deconvolution problem. Solutions for 1D deconvolution problem with different active subspace dimensions r = {1, 10}
and an overregularization parameter value α = 1e4. (Left) r = 1, uncentered approaches
are more robust to the regularization parameter since uncentered methods
do not penalize the data-informed direction. (Right) r = 10, all the DIAS
solutions are similar since all methods end up spanning the same subspace.
Figure 3: X-ray Tomography. Eigenvectors of uncentered AS wi and centered AS vi
, i = {1, 2, 6, 9} and their corresponding eigenvalues, noise level 1%. A striking difference between the first
eigenvector of the two active subspaces.
Figure 4: X-ray Tomography. DIAS solutions for X-ray tomography problem with overregularization parameter α = 1e8, noise level 1%.